Stress

What is stress? 

When a body gets deformed under the action of some external force, internal forces are set up within the body which tends to bring the body back to initial position. The magnitude of this internal force depends upon the deformation produced. Within a certain limit (called elastic limit-a limit up to which the material of a body posses the property of elasticity), the internal force is proportional to deformation produced. As deformation increases, the internal force also increases. At the equilibrium position, the internal force is equal in magnitude but opposite in direction to the deforming force.

This internal force per unit area of the deformed body is called stress. Because, in the equilibrium position, the internal restoring force is equal to the deforming force, hence quantitatively stress is equal to the deforming force acting per unit area of the deformed body. If F be the deforming force applied on a cross-sectional area A, we have Stress =F/A.
The cgs and SI units of stress are dynes cm^-2 and Nm^-2 respectively.

Different types of stress:

Depending upon the way, the deforming force is applied on a body, the stress may be:

a) Tensile stress

b) Tompressive stress

c) Tangential or shearing stress

d) Hydrostatic or volume stress

a) Tensile stress: 

The restoring force developed per unit cross-sectional area of a body, when the length of the body increases in the direction of deforming force, is called as tensile.
Suppose a rectangular body is fixed to a rigid support at the one end as shown in following figure. If we apply a force F outward at the free end, normally to its cross-sectional area A, an equal and opposite force (reaction) F comes into play at its fixed end, along the same line of action as shown in following figure. The body thus gets elongated i.e., the length of the body increases in the direction of force applied. The tensile stress developed inside the body is given by T=F/A.
Where A is the cross-sectional area of the body.

Tensile stress

b) Compressive stress: 

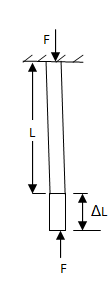
The restoring force developed per unit cross-sectional area of a body, when the body is compressed i.e., when its length decreases under the action of the deforming force, is called compressive.
Consider again a rectangular body fixed at one end to a rigid support as shown in following figure. If the force F be applied inwards at the free end of the body as of action and the body gets compressed i.e., its length decreases. In this case, therefore, compressive stress is given by T=F/A.
Where F represents a compressive force.

Compressive stress

c) Tangential or shearing stress:

 If the lower surface of a body is kept rigidly fixed and a deforming force F is applied tangentially to its upper surface of area A, As shown in following figure, an equal and opposite force F also starts acting on its lower fixed surface. Because th lines of action of two equal, opposite and parallel force are different, hence they form a couple which tries to rotate the body clockwise. As the lower surface of the body is kept fixed, the couple lead to twist in front face through an angle θ (as shown in figure), thus changing only the shape but not the volume of the body. The shearing is given by T= F/A.

Tangential or shearing stress

d) Hydrostatic or volume stress: 

When a body is subjected to a uniform force normally on all the faces, as shown in following figure, then the corresponding stress is called hydrostatic or volume. In this situation, shape of the body remains same but the volume gets changed. The hydrostatic is basically equal to hydrostatic pressure and is given by T= F/A=dP.

hydrostatic