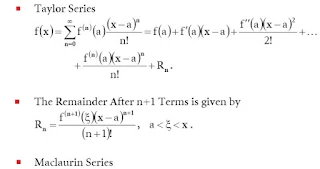Taylor and maclaurin series

Taylor and maclaurin series

In science, the Taylor arrangement of a capacity is an unending entirety of terms that are communicated as far as the capacity's subordinates at a solitary point. For most normal capacities, the capacity and the entirety of its Taylor arrangement are equivalent close to this point. Taylor's arrangement are named after Brook Taylor who presented them in 1715.

In the event that zero is where the subsidiaries are thought of, a Taylor arrangement is additionally called a Maclaurin arrangement, after Colin Maclaurin, who utilized this uncommon instance of Taylor arrangement in the eighteenth century.

The incomplete total framed by the n first terms of a Taylor arrangement is a polynomial of degree n that is known as the nth Taylor polynomial of the capacity. Taylor polynomials are approximations of a capacity, which become commonly better when n increments. Taylor's hypothesis gives quantitative evaluations on the blunder presented by the utilization of such approximations. In the event that the Taylor arrangement of a capacity is joined, its aggregate is the constraint of the interminable grouping of the Taylor polynomials. A capacity might be not equivalent to the entirety of its Taylor arrangement, regardless of whether its Taylor arrangement is united. A capacity is systematic at a point x in the event that it is equivalent to the aggregate of its Taylor arrangement in some open stretch (or open circle in the mind boggling plane) containing x. This suggests the capacity is systematic at each purpose of the span (or circle).